Podstawowe funkcje elementarne w czystej postaci bez transformacji są rzadkie, dlatego najczęściej trzeba pracować z funkcjami elementarnymi, które uzyskano z funkcji głównych poprzez dodanie stałych i współczynników. Wykresy takie konstruuje się wykorzystując przekształcenia geometryczne zadanych funkcji elementarnych.

Rozważmy przykład funkcji kwadratowej o postaci y = - 1 3 x + 2 3 2 + 2, której wykresem jest parabola y = x 2, która jest trzykrotnie ściśnięta względem Oy i symetryczna względem do Ox i przesunięty o 2 3 wzdłuż Ox w prawo, o 2 jednostki w górę wzdłuż Oy. Na linii współrzędnych wygląda to tak:

Yandex.RTB R-A-339285-1

Przekształcenia geometryczne wykresu funkcji

Stosując przekształcenia geometryczne danego wykresu otrzymujemy, że wykres przedstawia funkcja postaci ± k 1 · f (± k 2 · (x + a)) + b, gdy k 1 > 0, k 2 > 0 są współczynnikami kompresji wynoszącymi 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 wzdłuż O y i O x. Znak przed współczynnikami k 1 i k 2 wskazuje na symetryczne wyświetlanie wykresu względem osi, a i b przesuwają go wzdłuż O x i wzdłuż O y.

Definicja 1

Istnieją 3 typy przekształcenia geometryczne grafu:

• skalowanie wzdłuż O x i O y. Wpływ na to mają współczynniki k 1 i k 2, pod warunkiem, że nie są one równe 1, gdy wynoszą 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, wówczas wykres jest rozciągany wzdłuż O y i ściskany wzdłuż O x.
• Symetryczne wyświetlanie względem osi współrzędnych. Jeśli przed k 1 znajduje się znak „-”, symetria jest względem O x, a przed k 2 względem O y. Jeżeli brakuje „-”, element jest pomijany przy rozwiązywaniu;
• Transfer równoległy (przesunięcie) wzdłuż O x i O y. Transformację przeprowadza się, jeżeli istnieją współczynniki aib równe 0. Jeżeli a jest dodatnie, wykres zostaje przesunięty w lewo o | | jednostek, jeśli a jest ujemne, to w prawo w tej samej odległości. Wartość b określa ruch wzdłuż osi O y, co oznacza, że ​​gdy b jest dodatnie, funkcja przesuwa się w górę, a gdy b jest ujemne, przesuwa się w dół.

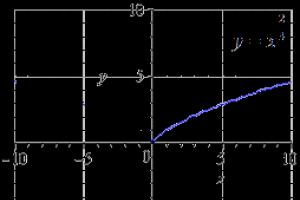
Przyjrzyjmy się rozwiązaniom na przykładach, zaczynając od funkcji potęgowej.

Przykład 1

Przekształć y = x 2 3 i wykreśl funkcję y = - 1 2 · 8 x - 4 2 3 + 3 .

Rozwiązanie

Przedstawmy funkcje w ten sposób:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Gdzie k 1 = 2, warto zwrócić uwagę na obecność „-”, a = - 1 2, b = 3. Stąd dowiadujemy się, że przekształcenia geometryczne przeprowadza się poprzez dwukrotne rozciąganie wzdłuż O y, wyświetlane symetrycznie względem O x, przesunięte w prawo o 1 2 i w górę o 3 jednostki.

Jeśli przedstawimy pierwotną funkcję potęgową, otrzymamy to

po rozciągnięciu dwukrotnie wzdłuż O y, mamy to

Odwzorowanie symetryczne względem Ox ma postać

i przesuń się w prawo o 1 2

wygląda ruch o 3 jednostki w górę

Przyjrzyjmy się przekształceniom funkcji wykładniczych na przykładach.

Przykład 2

Skonstruuj wykres funkcji wykładniczej y = - 1 2 1 2 (2 - x) + 8.

Rozwiązanie.

Przekształćmy funkcję w oparciu o właściwości funkcji potęgowej. Wtedy to zrozumiemy

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Widzimy z tego, że otrzymujemy łańcuch transformacji y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Stwierdzamy, że pierwotna funkcja wykładnicza ma postać

Ściśnięcie dwukrotnie wzdłuż O y daje

Rozciąganie wzdłuż O x

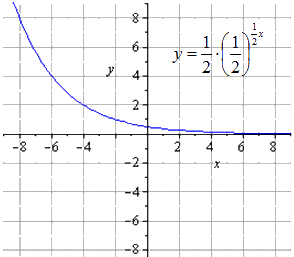
Mapowanie symetryczne względem O x

Mapowanie jest symetryczne względem O y

Przejdź w górę o 8 jednostek

Rozważmy rozwiązanie na przykładzie funkcji logarytmicznej y = ln (x).

Przykład 3

Skonstruuj funkcję y = ln e 2 · - 1 2 x 3, korzystając z transformacji y = ln (x) .

Rozwiązanie

Aby rozwiązać, konieczne jest skorzystanie z właściwości logarytmu, a następnie otrzymamy:

y = ln mi 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Transformacje funkcji logarytmicznej wyglądają następująco:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Narysujmy pierwotną funkcję logarytmiczną

Kompresujemy system zgodnie z O y

Rozciągamy się wzdłuż O x

Wykonujemy mapowanie względem O y

Przesuwamy się w górę o 2 jednostki i otrzymujemy

Aby przekształcić wykresy funkcji trygonometrycznej, należy dopasować do schematu rozwiązania postaci ± k 1 · f (± k 2 · (x + a)) + b. Konieczne jest, aby k 2 było równe T k 2 . Stąd otrzymujemy to 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Spójrzmy na przykłady rozwiązywania problemów z transformacjami y = sin x.

Przykład 4

Skonstruuj wykres y = - 3 sin 1 2 x - 3 2 - 2 korzystając z przekształceń funkcji y=sinx.

Rozwiązanie

Należy sprowadzić funkcję do postaci ± k 1 · f ± k 2 · x + a + b. Dla tego:

y = - 3 grzech 1 2 x - 3 2 - 2 = - 3 grzech 1 2 (x - 3) - 2

Można zauważyć, że k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Ponieważ przed k 1 jest „-”, ale nie przed k 2, to otrzymujemy łańcuch przekształceń postaci:

y = grzech (x) → y = 3 grzech (x) → y = 3 grzech 1 2 x → y = - 3 grzech 1 2 x → → y = - 3 grzech 1 2 x - 3 → y = - 3 grzech 1 2 (x - 3) - 2

Szczegółowa transformacja fali sinusoidalnej. Wykreślając pierwotną sinusoidę y = sin (x), stwierdzamy, że za najmniejszy dodatni okres uważa się T = 2 π. Znalezienie maksimum w punktach π 2 + 2 π · k; 1, a minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y zostanie rozciągnięty trzykrotnie, co oznacza, że ​​wzrost amplitudy oscylacji wzrośnie 3-krotnie. T = 2 π to najmniejszy okres dodatni. Maksima idą do π 2 + 2 π · k; 3, k ∈ Z, minima - - π 2 + 2 π · k; - 3, k ∈ Z.

Rozciągając się wzdłuż O x o połowę, stwierdzamy, że najmniejszy dodatni okres zwiększa się 2 razy i jest równy T = 2 π k 2 = 4 π. Maksima wynoszą π + 4 π · k; 3, k ∈ Z, minima – in - π + 4 π · k; - 3, k ∈ Z.

Obraz jest tworzony symetrycznie względem Ox. Najmniejszy okres dodatni w tym przypadku nie ulega zmianie i wynosi T = 2 π k 2 = 4 π. Maksymalne przejście wygląda - π + 4 π · k; 3, k ∈ Z, a minimum to π + 4 π · k; - 3, k ∈ Z.

Wykres jest przesunięty w dół o 2 jednostki. Minimalny okres wspólny nie ulega zmianie. Znajdowanie maksimów z przejściem do punktów - π + 3 + 4 π · k; 1, k ∈ Z, minimum - π + 3 + 4 π · k; - 5 , k ∈ Z .

Na tym etapie wykres funkcji trygonometrycznej uważa się za przekształcony.

Rozważmy szczegółową transformację funkcji y = cos x.

Przykład 5

Skonstruuj wykres funkcji y = 3 2 cos 2 - 2 x + 1, korzystając z transformacji funkcji w postaci y = cos x.

Rozwiązanie

Zgodnie z algorytmem należy daną funkcję sprowadzić do postaci ± k 1 · f ± k 2 · x + a + b. Wtedy to zrozumiemy

y = 3 2 sałata 2 - 2 x + 1 = 3 2 sałata (- 2 (x - 1)) + 1

Z warunku jasno wynika, że ​​k 1 = 3 · 2, k 2 = 2, a = - 1, b = 1, gdzie k 2 ma „-”, ale przed k 1 jest nieobecny.

Widzimy z tego, że otrzymujemy wykres funkcji trygonometrycznej postaci:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1 )) → y = 3 2 sałata - 2 (x - 1) + 1

Transformacja cosinusowa krok po kroku z ilustracją graficzną.

Biorąc pod uwagę wykres y = cos(x), jasne jest, że najkrótszy całkowity okres to T = 2π. Znajdowanie maksimów w 2 π · k ; 1, k ∈ Z i są minima π + 2 π · k; - 1, k ∈ Z.

Po rozciągnięciu wzdłuż Oy 3 2 razy amplituda oscylacji wzrasta 3 2 razy. T = 2 π to najmniejszy okres dodatni. Znajdowanie maksimów w 2 π · k ; 3 2, k ∈ Z, minima w π + 2 π · k; - 3 2 , k ∈ Z .

Po skompresowaniu wzdłuż O x o połowę okazuje się, że najmniejszym okresem dodatnim jest liczba T = 2 π k 2 = π. Następuje przejście maksimów do π · k; 3 2 , k ∈ Z , minima - π 2 + π · k ; - 3 2 , k ∈ Z .

Mapowanie symetryczne w odniesieniu do Oy. Ponieważ wykres jest nieparzysty, nie ulegnie on zmianie.

Gdy wykres zostanie przesunięty o 1. Nie ma zmian w najmniejszym okresie dodatnim T = π. Znajdowanie maksimów w π · k + 1 ; 3 2, k ∈ Z, minimum - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Po przesunięciu o 1 najmniejszy okres dodatni jest równy T = π i nie ulega zmianie. Znajdowanie maksimów w π · k + 1 ; 5 2, k ∈ Z, minima w π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Transformacja funkcji cosinus została zakończona.

Rozważmy transformacje na przykładzie y = t g x.

Przykład 6

Skonstruuj wykres funkcji y = - 1 2 t g π 3 - 2 3 x + π 3 korzystając z przekształceń funkcji y = t g (x) .

Rozwiązanie

Na początek należy sprowadzić daną funkcję do postaci ± k 1 · f ± k 2 · x + a + b, po czym otrzymujemy, że

y = - 1 2 t sol π 3 - 2 3 x + π 3 = - 1 2 t sol - 2 3 x - π 2 + π 3

Wyraźnie widać, że k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, a przed współczynnikami k 1 i k 2 jest „-”. Oznacza to, że po przekształceniu stycznych otrzymamy

y = t sol (x) → y = 1 2 t g (x) → y = 1 2 t sol 2 3 x → y = - 1 2 t sol 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Transformacja stycznych krok po kroku z przedstawieniem graficznym.

Wiemy, że pierwotny wykres to y = t g (x) . Zmiana okresu dodatniego jest równa T = π. Za dziedzinę definicji uważa się - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Ściskamy go 2 razy wzdłuż Oy. Za najmniejszy okres dodatni uważa się T = π, którego dziedzina definicji ma postać - π 2 + π · k; π 2 + π · k, k ∈ Z.

Rozciągnij wzdłuż O x 3 2 razy. Obliczmy najmniejszy okres dodatni, który był równy T = π k 2 = 3 2 π . A dziedzina definicji funkcji ze współrzędnymi to 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, zmienia się jedynie dziedzina definicji.

Symetria idzie po stronie O x. Okres ten nie ulegnie w tym momencie zmianie.

Konieczne jest symetryczne wyświetlanie osi współrzędnych. Dziedzina definicji w tym przypadku pozostaje niezmieniona. Harmonogram pokrywa się z poprzednim. Sugeruje to, że funkcja tangensa jest nieparzysta. Jeśli przypiszemy symetryczne odwzorowanie O x i O y funkcji nieparzystej, wówczas przekształcimy ją do funkcji pierwotnej.

Rozwiązanie

Najpierw musisz przejść od arcus cosinus do arcus sinus, używając odwrotnych funkcji trygonometrycznych a r c sin x + a r c o cos x = π 2. Oznacza to, że otrzymujemy, że a r c sin x = π 2 - a r do cos x.

Można zauważyć, że y = za r do cos x → y = - a r do cos x → y = - a r do cos x + π 2.

Transformacja arccosinusa krok po kroku i reprezentacja graficzna.

Harmonogram podany według warunku

Wykonujemy mapowanie względem Ox

Przesuwamy się w górę o π 2.

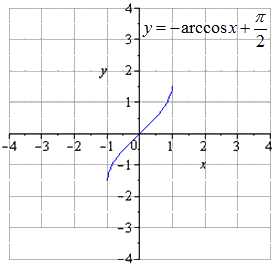
W ten sposób dokonuje się przejścia od arc cosinus do cosinus. Należy wykonać przekształcenia geometryczne arcus sinusa i jego wykresu.

Można zauważyć, że k 1 = 2, k 2 = 1 3, a = - 1, b = 0, gdzie brakuje znaku „-” dla k 1 i k 2.

Z tego wynika, że ​​transformacja y = a r c sin x ma postać:

y = za r do grzech (x) → y = 2 za r do grzech (x) → → y = 2 za r do grzech 1 3 x → y = 2 za r do grzech 1 3 (x - 1)

Transformacja krok po kroku wykresu łuku sinusoidalnego i przedstawienie graficzne.

Wykres y = a r do sin x ma dziedzinę postaci x ∈ - 1 ; 1, następnie przedział y ∈ - π 2; π 2 należy do zakresu wartości.

Należy go dwukrotnie rozciągnąć wzdłuż O y, a dziedzina definicji pozostanie niezmieniona x ∈ - 1; 1 i zakres wartości y ∈ - π; π.

Rozciąganie według struktury Ox. Rozszerzono dziedzinę definicji x ∈ - 3; 3, ale zakres wartości pozostaje niezmieniony y ∈ - π; π.

Która z tych funkcji ma odwrotność? Dla takich funkcji znajdź funkcje odwrotne:

4.12. A)	y = x ;					b) y = 6 −3 x ;
d) y =						e) y = 2 x 3 +5;
4.13. A)	y = 4 x - 5 ;						y = 9 - 2 x - x 2 ;
	y = znak x ;						y =1 + log(x + 2) ;

	y = 2 x 2 +1 ;
			x - 2
						o x< 0
c) y =		−x
						dla x ≥ 0

Dowiedz się, które z tych funkcji są monotoniczne, które ściśle monotoniczne, a które ograniczone:

4.14. A)

fa (x) = do, do R ;

b) fa (x) = cos 2 x;

c) fa (x) = arctan x;

d) fa (x) = mi 2 x;

e) fa (x) = −x 2 + 2 x;

e) fa (x) =

2x+5

y = ctg7 x .

4.15. A)

f(x) = 3− x

b) f(x) =

f(x)=

x+3

x+6

X< 0,

3x+5

d) fa (x) = 3 x 3 - x;

− 10 o godz

f(x)=

e) fa (x) =

x 2 godz

x ≥ 0;

x+1

f (x) = tan(sin x).

4.2. Funkcje elementarne. Konwersja wykresów funkcji

Przypomnijmy, że wykres funkcji f(x) w kartezjańskim prostokątnym układzie współrzędnych Oxy jest zbiorem wszystkich punktów płaszczyzny o współrzędnych (x, f(x)).

Często wykres funkcji y = f (x) można zbudować wykorzystując przekształcenia (przesunięcie, rozciągnięcie) wykresu jakiejś już znanej funkcji.

W szczególności z wykresu funkcji y = f (x) uzyskuje się wykres funkcji:

1) y = f (x) + a – przesunięcie wzdłuż osi Oy o jednostki (w górę, jeśli a > 0 i w dół, jeśli a< 0 ;

2) y = f (x −b) – przesunięcie wzdłuż osi Ox o jednostki b (w prawo, jeśli b > 0,

i wyszedł, jeśli b< 0 ;

3) y = kf (x) – rozciąganie wzdłuż osi Oy k razy;

4) y = f (mx) – ściśnięcie wzdłuż osi Wół m-krotne;

5) y = − f (x) – odbicie symetryczne względem osi Wółu;

6) y = f (−x) – odbicie symetryczne względem osi Oy;

7) y = f (x), jak następuje: część wykresu nie zlokalizowana

poniżej osi Wółu pozostaje niezmieniona, a „dolna” część wykresu jest odzwierciedlona symetrycznie względem osi Wółu;

8) y = f (x), jak następuje: prawa strona wykresu (dla x ≥ 0)

pozostaje niezmieniona, a zamiast „lewego” skonstruowane jest symetryczne odbicie „prawego” względem osi Oy.

Główne funkcje elementarne nazywane są:

1) funkcja stała y = c;

2) funkcja potęgowa y = x α , α R ;

3) funkcja wykładnicza y = a x, a ≠ 0, a ≠1;

4) logarytmiczny funkcja y = log a x , a > 0, a ≠ 1 ;

5) trygonometryczny funkcje y = sin x, y = cos x, y = tan x,

y = ctg x, y = sec x (gdzie sec x = cos 1 x), y = cosec x (gdzie cosec x = sin 1 x);

6) odwrotne funkcje trygonometryczne y = arcsin x, y = arccos x, y = arctan x, y = arcctg x.

Funkcje elementarne nazywane są funkcjami otrzymanymi z podstawowych funkcji elementarnych za pomocą skończonej liczby operacji arytmetycznych (+, -, ÷) i złożeniami (tj. tworzeniem funkcji zespolonych f g).

Przykład 4.6. Wykres funkcji

1) y = x 2 + 6 x + 7 ; 2) y = −2sin 4 x .

Rozwiązanie: 1) wybierając pełny kwadrat, funkcja zostaje przekształcona do postaci y = (x +3) 2 − 2, zatem wykres tej funkcji można otrzymać z wykresu funkcji y = x 2. Wystarczy najpierw przesunąć parabolę y = x 2 o trzy jednostki w lewo (otrzymujemy wykres funkcji y = (x +3) 2), a następnie o dwie jednostki w dół (ryc. 4.1);

	standard	sinusoida						y = grzech x	cztery razy wzdłuż osi		Wół,
otrzymujemy wykres funkcji y = sin 4 x (ryc. 4.2).
										y=grzech4x
										y=grzech x

Rozciągając powstały wykres dwukrotnie wzdłuż osi Oy, otrzymujemy wykres funkcji y = 2sin 4 x (ryc. 4.3). Pozostaje wyświetlić ostatni wykres względem osi Wołu. Rezultatem będzie pożądany wykres (patrz ryc. 4.3).

						y=2sin4x

y=– 2sin4 x

Problemy do samodzielnego rozwiązania

Konstruuj wykresy następujących funkcji na podstawie wykresów podstawowych funkcji elementarnych:

4.16. a) y = x 2 −6 x +11 ;

4.17. a) y = −2sin(x −π ) ;

4.18. a) y = - 4 x -1 ;

4.19. a) y = log 2 (-x);

4.20. a) y = x +5;

4.21. a) y = tg x ;

4.22. a) y = znak x;

4.23. a) y = x x + + 4 2 ;

y = 3 - 2 x - x 2 .

y = 2cos 2 x .

, Konkurs „Prezentacja na lekcję”

Prezentacja na lekcję

Powrót do przodu

Uwaga! Podglądy slajdów służą wyłącznie celom informacyjnym i mogą nie odzwierciedlać wszystkich funkcji prezentacji. Jeśli jesteś zainteresowany tą pracą, pobierz pełną wersję.

Cel lekcji: Wyznaczać wzory transformacji wykresów funkcji.

Zadania:

Edukacyjny:

• Nauczenie studentów konstruowania wykresów funkcji poprzez przekształcenie wykresu danej funkcji, zastosowanie translacji równoległej, kompresji (rozciągania) i różnych rodzajów symetrii.

Edukacyjny:

• Kultywowanie cech osobistych uczniów (umiejętność słuchania), życzliwości wobec innych, uważności, dokładności, dyscypliny i umiejętności pracy w grupie.
• Pielęgnuj zainteresowanie tematem i potrzebę zdobywania wiedzy.

Rozwojowy:

• Rozwijanie wyobraźni przestrzennej i logicznego myślenia uczniów, umiejętności szybkiego poruszania się po otoczeniu; rozwijać inteligencję, zaradność i ćwiczyć pamięć.

Sprzęt:

• Instalacja multimedialna: komputer, projektor.

Literatura:

1. Bashmakov, M. I. Matematyka [Tekst]: podręcznik dla początkujących instytucji. i środa prof. edukacja / M.I. Bashmakov - wydanie 5, poprawione. – M.: Centrum Wydawnicze „Akademia”, 2012. – 256 s.
2. Bashmakov, MI Matematyka. Książka problemowa [Tekst]: podręcznik. dodatek na naukę instytucje wcześnie i środa prof. edukacja / M. I. Bashmakov – M.: Centrum Wydawnicze „Akademia”, 2012. – 416 s.

Plan lekcji:

1. Chwila organizacyjna (3 min).
2. Aktualizacja wiedzy (7 min).
3. Wyjaśnienie nowego materiału (20 min).
4. Utrwalenie nowego materiału (10 min).
5. Podsumowanie lekcji (3 min).
6. Praca domowa (2 min).

Podczas zajęć

1. Org. chwilę (3 minuty).

Sprawdzanie obecnych.

Przekaż cel lekcji.

Podstawowe właściwości funkcji jako zależności między wielkościami zmiennymi nie powinny ulegać istotnym zmianom przy zmianie sposobu pomiaru tych wielkości, czyli zmianie skali pomiaru i punktu odniesienia. Jednak dzięki bardziej racjonalnemu wyborowi metody pomiaru wielkości zmiennych zwykle udaje się uprościć rejestrację zależności między nimi i doprowadzić ten zapis do jakiejś standardowej postaci. W języku geometrycznym zmiana sposobu pomiaru wartości oznacza kilka prostych przekształceń wykresów, które dzisiaj przestudiujemy.

2. Aktualizacja wiedzy (7 min).

Zanim porozmawiamy o przekształceniach grafów, przejrzyjmy omawiany przez nas materiał.

Praca ustna. (slajd 2).

Podane funkcje:

3. Opisz wykresy funkcji: , , , .

3. Wyjaśnienie nowego materiału (20 min).

Najprostsze przekształcenia grafów to ich równoległe przenoszenie, ściskanie (rozciąganie) i niektóre rodzaje symetrii. Niektóre przekształcenia przedstawiono w tabeli (Aneks 1), (slajd 3).

Praca w grupach.

Każda grupa konstruuje wykresy zadanych funkcji i przedstawia wynik do dyskusji.

Funkcjonować	Przekształcanie wykresu funkcji	Przykłady funkcji	Slajd
	Jednostka organizacyjna NA A jednostki w górę, jeśli A>0 i na |A| jednostki w dół, jeśli A<0.	,	(slajd 4)
	Przenoszenie równoległe wzdłuż osi Oh NA A jednostki po prawej stronie jeśli A>0 i dalej - A jednostki po lewej stronie if A<0.	,	(slajd 5)
,

Konwersja wykresów funkcji

W tym artykule przedstawię Państwu przekształcenia liniowe wykresów funkcyjnych oraz pokażę jak za pomocą tych przekształceń otrzymać wykres funkcji z wykresu funkcji

Transformacja liniowa funkcji to transformacja samej funkcji i/lub jej argumentu do postaci , a także transformację zawierającą argument i/lub moduł funkcji.

Największe trudności przy konstruowaniu wykresów za pomocą przekształceń liniowych powodują następujące działania:

1. Izolując podstawową funkcję, której wykres przekształcamy.
2. Definicje rzędu przekształceń.

I Właśnie w tych punktach zajmiemy się bardziej szczegółowo.

Przyjrzyjmy się bliżej funkcji

Opiera się na funkcji. Zadzwońmy do niej podstawowa funkcja.

Podczas kreślenia funkcji dokonujemy przekształceń na wykresie funkcji bazowej.

Gdybyśmy mieli dokonać przekształceń funkcji wówczas w tej samej kolejności, w jakiej znaleziono jego wartość dla określonej wartości argumentu

Zastanówmy się, jakie rodzaje transformacji liniowych argumentu i funkcji istnieją i jak je przeprowadzić.

Przekształcenia argumentów.

1. f(x) f(x+b)

1. Zbuduj wykres funkcji

2. Przesuń wykres funkcji wzdłuż osi OX o |b| jednostki

• pozostawiony, jeśli b>0
• prawda, jeśli b<0

Narysujmy funkcję

1. Zbuduj wykres funkcji

2. Przesuń go o 2 jednostki w prawo:

2. f(x) f(kx)

1. Zbuduj wykres funkcji

2. Podziel odcięte punktów wykresu przez k, pozostawiając rzędne punktów bez zmian.

Zbudujmy wykres funkcji.

1. Zbuduj wykres funkcji

2. Podziel wszystkie odcięte punktów wykresu przez 2, pozostawiając rzędne bez zmian:

3. f(x) f(-x)

1. Zbuduj wykres funkcji

2. Wyświetl go symetrycznie względem osi OY.

Zbudujmy wykres funkcji.

1. Zbuduj wykres funkcji

2. Wyświetl go symetrycznie względem osi OY:

4. f(x) fa(|x|)

1. Zbuduj wykres funkcji

2. Wymazuje się część wykresu znajdującą się na lewo od osi OY, część wykresu znajdującą się na prawo od osi OY uzupełnia się symetrycznie względem osi OY:

Wykres funkcji wygląda następująco:

Narysujmy funkcję

1. Budujemy wykres funkcji (jest to wykres funkcji przesunięty wzdłuż osi OX o 2 jednostki w lewo):

2. Część wykresu zlokalizowana na lewo od osi OY (x).<0) стираем:

3. Uzupełniamy część wykresu znajdującą się na prawo od osi OY (x>0) symetrycznie względem osi OY:

Ważny! Dwie główne zasady przekształcania argumentu.

1. Wszystkie transformacje argumentów wykonywane są wzdłuż osi OX

2. Wszelkie przekształcenia argumentu wykonujemy „odwrotnie” i „w odwrotnej kolejności”.

Przykładowo w funkcji kolejność transformacji argumentów jest następująca:

1. Weź moduł x.

2. Dodaj liczbę 2 do modulo x.

Ale skonstruowaliśmy wykres w odwrotnej kolejności:

Najpierw wykonano transformację 2 - wykres przesunięto o 2 jednostki w lewo (czyli odcięte punktów zmniejszono o 2, jakby „na odwrót”)

Następnie wykonaliśmy transformację f(x) f(|x|).

W skrócie sekwencję przekształceń zapisuje się następująco:

Teraz porozmawiajmy o transformacja funkcji . Następują przemiany

1. Wzdłuż osi OY.

2. W tej samej kolejności, w jakiej wykonywane są czynności.

Oto przekształcenia:

1. f(x)f(x)+D

2. Przesuń go wzdłuż osi OY o |D| jednostki

• w górę, jeśli D > 0
• w dół, jeśli D<0

Narysujmy funkcję

1. Zbuduj wykres funkcji

2. Przesuń go wzdłuż osi OY o 2 jednostki w górę:

2. f(x)Af(x)

1. Zbuduj wykres funkcji y=f(x)

2. Mnożymy rzędne wszystkich punktów wykresu przez A, pozostawiając odcięte bez zmian.

Narysujmy funkcję

1. Zbudujmy wykres funkcji

2. Pomnóż współrzędne wszystkich punktów na wykresie przez 2:

3.f(x)-f(x)

1. Zbuduj wykres funkcji y=f(x)

Zbudujmy wykres funkcji.

1. Zbuduj wykres funkcji.

2. Wyświetlamy go symetrycznie względem osi OX.

4. f(x)|f(x)|

1. Zbuduj wykres funkcji y=f(x)

2. Część wykresu znajdującą się powyżej osi OX pozostawiamy bez zmian, część wykresu znajdująca się poniżej osi OX wyświetlana jest symetrycznie względem tej osi.

Narysujmy funkcję

1. Zbuduj wykres funkcji. Uzyskuje się to poprzez przesunięcie wykresu funkcji wzdłuż osi OY o 2 jednostki w dół:

2. Teraz wyświetlimy część wykresu znajdującą się poniżej osi OX symetrycznie względem tej osi:

I ostatnia transformacja, której, ściśle rzecz biorąc, nie można nazwać transformacją funkcyjną, ponieważ wynik tej transformacji nie jest już funkcją:

|y|=f(x)

1. Zbuduj wykres funkcji y=f(x)

2. Wymazujemy część wykresu znajdującą się poniżej osi OX, następnie uzupełniamy część wykresu znajdującą się powyżej osi OX symetrycznie względem tej osi.

Ułóżmy równanie

1. Budujemy wykres funkcji:

2. Wymazujemy część wykresu znajdującą się poniżej osi OX:

3. Uzupełniamy część wykresu znajdującą się nad osią OX symetrycznie względem tej osi.

Na koniec proponuję obejrzeć TUTORIAL WIDEO, w którym pokazuję krok po kroku algorytm konstruowania wykresu funkcji

Wykres tej funkcji wygląda następująco: